Direct Measurements Calculator

Measurements

# Values Actions

Settings

Results

Result Value
Average value \(\bar{x}\) 0
Standard error, \(s_{x}\) 0
Random error, \(\Delta x_{s}\) 0
Device error, \(\delta_{x}\) 0
Measurement error, \(\Delta x_{\delta}\) 0
Absolute error, \(\Delta x\) 0
Relative error, \(\varepsilon\) 0

Final Result:

  \(x\) = 0 \(\pm\) 0 [unit],
  \(\varepsilon\) = 0%, at
  \(\beta\) = 0.95

Guide

There are two different values that can describe a quantity: true value and real value.

True value is theoretical measure of something that describes exact value. This value has unlimited precision and none of the errors - exists only in ideal world.

Real value - experimentally defined value of physical quantity, which is approaching the true value so close that can replace it in calculations. Real value describes quantity with limited accuracy, thus with certain probability and estimated error.

Sources of error can be divided in three groups:

  1. mistakes
  2. systematic errors:
    1. corrections
    2. device error
    3. object’s error
  3. random errors

In general case all mentioned errors construct the absolute error of the measurement result.

Student Coefficient Table

Student Coefficient Table

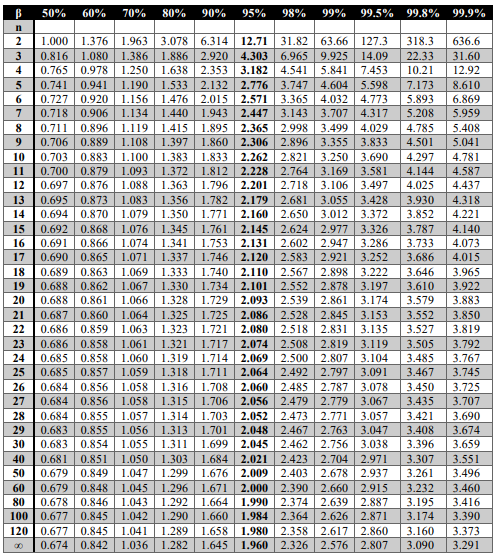
Take into account that for "Random error" we use Students coefficient for our number of measurements, however, "Measurement error" is being calculated by using Students coefficient for infinity. This is done due to the fact that we assume that measurement instrument is guaranteed to work with certain accuracy and all the variance should be caused only by the decision of choosing closest value on the scale of instrument.